I have written earlier on the action of air pressure in tires. A similarly non-intuitive question is that of pressure distribution inside a lighter-than-air balloon. While we typically think of the gas pressure inside a sealed container as being a single value, to explain the flotation of a balloon filled with a gas less dense than the surrounding air we have to consider the gravitational pressure differential within said container, so the pressure is to be seen as a function of height in a gravitational well even on centimeter scales. If we enclose a tall column of air, and measure the pressure inside this column relative to the outside, we will get a zero value at all heights, because the change of pressure with height above the ground is equal inside and outside the column. If we replace the air inside the column with a different density gas, the change of pressure with height will be unequal inside and outside the column; we may set a reference height where the pressures are equal, and they will diverge with distance away from this height. In the limiting case, the column would contain a vacuum, and then we can measure the absolute atmospheric pressure, which is a function of height - the principle of the barometer. When reading a pressure in a weather forecast, a difference is to be recognized between the absolute pressure measured at a weather station (which depends on elevation as well as atmospheric patterns), and said pressure adjusted to a standard elevation, allowing more meaningful comparisons with other stations. By the same principle, a portable barometer can be used to measure changes in elevation - this is a standard instrument in aircraft and is also seen in some sports watches, where changes on the order of 1 meter can be distinguished.
Then, how does the absolute pressure depend on altitude? If the pressure at some altitude z is P(z), then P(z-dz)=P(z)+rho(z)*dz, that is the pressure increases with decreasing altitude based on fluid density. (We assume the change in gravitational acceleration as a function of height is relatively small.) The density in turn depends on pressure, as (N/V)=P/(RT) for an ideal gas; we can combine the other values into one factor J so that J=rho(z)/P(z) is a constant for a given gas. Then, P(z-dz)=P(z)*(1+J*dz) and dP(z)/dz=(P(z)-P(z-dz))/dz=-P(z)*J. This gives an exponential solution:
P(z)=P0*exp(-J*z)
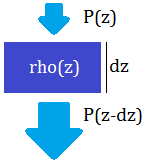
Illustration of how a small layer of gas adds its weight as pressure to the lower gas layers, resulting in the pressure increasing exponentially as altitude decreases.
As a side note, exponential functions are not often so plainly visible in nature, because they can rapidly span orders of magnitude and exceed limits of a given phenomenon. Some other interesting cases are the force differential between two ends of a rope wound around a cylinder (see also the torque amplifier), thermally activated reactions (Arrhenius reactions), population growth, and control of a nuclear reactor. On the topic of radiation, the intensity of radiation traveling through a constant density material decays exponentially; radiation coming from outer space towards the earth travels through the atmosphere where the density rises exponentially, hence the level of cosmic radiation as a function of elevation is "doubly exponential" - strongly dependent on elevation - as I have measured earlier.
For air at 101325 Pa and 20 degC, the density is about 1.204 kg/m^3 which is 11.81 N/m^3, so J2=0.000117 m^-1. This means that the pressure reduces to half of its value in a rise of 5.92 km. For hydrogen at similar conditions, the figure is 0.81 N/m^3, so J1=0.000008 m^-1, and the pressure reduces to half of its value in a rise of 86.6 km. These distances do not perfectly apply to the atmosphere because the temperature of the upper layers will be lower than 20 degC, however the numbers still apply to smaller scales. In a rise of 1 m, the pressure of air is 0.999883 that of base, and hydrogen is 0.999992 that of base. Thus if we have a 1 m tall cylinder filled with hydrogen, and the pressure at the bottom of the cylinder is equal to that of the surrounding air, the pressure at the top will be higher than that of the surrounding air - because the hydrogen does not apply as much weight onto the lower volume of the cylinder (compared to what air would do) so there is more force remaining to be transmitted upwards. The difference will be dP=P0*(exp(-J1*H)-exp(-J2*H)), where P0 is the base pressure at the bottom of the cylinder, J1,J2 are the different density factors for the two gases, and H is the height of the cylinder. Because realistic values of H will be much smaller than the km scales seen above, we can substitute a linearized expression: dP=P0*(J2-J1)*H with a base pressure P0. The total force will depend on the cylinder cross-sectional area A, as F=dP*A; the surface area of the cylinder will be S=2*A+k*H*sqrt(A), where k depends on the shape of the cylinder (4 for square, 3.545 for circle). A simple Scilab script that includes the above formulas may be downloaded here.
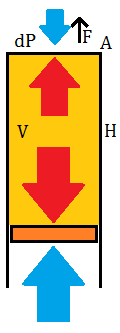
A vertical cylinder sealed at the top end and with a massless piston to seal the bottom end while keeping the pressure of the internal gas equal to the surrounding air at the bottom of the cylinder. In this case, the gas inside the cylinder will transmit its pressure more effectively to the top surface, so a pressure differential will exist there. This results in an upward force on the cylinder. Air pressure is indicated with blue arrows and gas pressure in the cylinder is indicated with red arrows.
We may ask: with a constant cylinder volume (V=H*A), does the cylinder shape make a difference to the total upwards force? F=dP*(V/H)=P0*(J2-J1)*V, using the linearized version of dP, so the upwards force is constant regardless of cylinder shape. (If the exponential version of dP is used, then the upwards force is highest for short cylinders (low H/A) and decreases for tall cylinders, with the difference noticeable only when the cylinder height is on the scale of 1000 m.) Then we can expect that the best performance in terms of upwards force per surface area, with a given volume of gas, will be obtained with a spherical balloon. The actual shape of a balloon whose pressure is not set by the surface stretching is probably a complicated matter to calculate, but it should take on the "inverted teardrop" shape of newly released weather balloons. There, the amount of gas is not sufficient to fill the internal volume of the balloon, so the lower portion of the balloon matches the surrounding atmospheric pressure of air, while the upper portion is relatively pressurized because the internal gas carries more of the lower side pressure to the top, and this difference in pressure exerts the upwards force on the balloon surface material and any attached objects, lifting them up into the atmosphere.

A model of a lighter than air balloon that is not externally pressurized: a non-stretchy but deformable material holds the gas in the "inverted teardrop" shape. A pressure difference arises on the top surface, which pulls the balloon upwards.
Further, if instead of a constant volume, we have a constant gas mass M=rho(z)*V(z)=P(z)*J1*V(z), then V(z)=M/(J1*P(z)), and F=P(z)*(J2-J1)*M/(J1*P(z))=M*(J2/J1-1). (Assuming the balloon size is small relative to the exponential scale distances, then set P0=P(z) as the balloon rises and we can keep using the linearized expression; M may be expressed in Newtons so the units match.) Thus, for an under-filled weather balloon released from the ground, so long as V(z) can increase with altitude to match the surrounding air pressure, the upwards force F will be constant. With the above values for hydrogen and air, J2/J1-1=13.6, meaning the upwards force is 13.6 times the mass of hydrogen in the balloon. For helium (J1=0.000016 m^-1) and air, the ratio is 6.37, but a helium atom weighs twice as much as a hydrogen molecule so a balloon will perform similarly with either gas. (With the same fill volume, hydrogen will provide about 1.08 times the upward force of helium.)
Compressibility is how much the volume of an object changes as the surrounding pressure is increased, C=d(rho)/dP=J if using the coefficients defined above. Thus in some sense, the reason a gas like hydrogen or helium can be used for lifting is that it is less compressible than air. Water is also less compressible than air, but it is much denser to start with so the analogy doesn't apply (the derivative applied for C requires a rho0 term when inverted, and this is higher for water). Rubber or gel is at first glance an exemplary compressible material but this is inaccurate: rubber is soft and squishy when there is an opportunity for it to deform into a zone of lower pressure, but if rubber is put into a cylinder and compressed (or compressed on all sides by a surrounding fluid) its change in volume is low. (Something that has given me pause is trying to explain how it is possible to slurp or "suck in" a long noodle even though it is not possible to push on a string.) What I want to relate in the context of the balloon discussion is that to float stably within a fluid an object must have a lower compressibility than the fluid. The best freedom of movement can be achieved in "true flotation", where the surrounding fluid exerts no force on the object vertically but the height of the object may change depending on other applied forces. The difference between "true flotation" and neutral buoyancy is that while both require the object to match the surrounding fluid density, "true flotation" also requires the object to match the surrounding fluid compressibility or the change of density with height. Then the object is indistinguishable from the surrounding fluid in the gravitational well and may move around freely. This is seldom accomplished, and instead neutral buoyancy is achieved by controlling some aspect of the object to match the surrounding fluid density at the object's altitude, then if a change in altitude occurs, the object must adjust its density to again match the fluid.
A helium-filled dirigible floats upwards and contains the gas inside the balloon, so operating under a constant volume rather than constant mass condition. Unlike the weather balloon propelled by a constant upward force until bursting, the dirigible reaches an altitude where the density of the object (with the gas now compressed inside the structure) matches the density of the atmosphere, and because the gas is less compressible than air, the object can remain at that altitude. If it exceeds the altitude where the densities match, it will fall downwards to again reach that altitude. By releasing or compressing the gas, a controlled descent may be achieved. The situation is very different for submarines, divers, and fishes, which use air to achieve flotation in water. Because air is more compressible than water, the flotation of these objects is unstable: if they go above the equal-density depth they will be pulled further up, and if they go below the equal-density depth they will be pushed further down. This is why divers are instructed to never hold their breath, and why dead fish are seen on the water surface (those that die and fall towards the bottom are not so easily seen). Some "Galileo thermometers", with floating objects in a column of fluid, seemingly defy the unstable situation presented above by using a mixture of transparent fluids, which increases the gradient of density with depth and therefore the effective "compressibility" of the fluid to the point that it is lower than the floating objects and stability is restored. The "Cartesian diver" toy makes for a clearer demonstration of the flotation instability: the diver can be maintained at an intermediate depth of the fluid column only by actively controlling the pressure of the fluid.