On a playground swing, from experience it appears possible for the rider to gain angular momentum without touching the ground. How is this possible, and can it be proven that a rider starting from a zero-motion state can accelerate to a high swing amplitude? In a purely rotating reference frame (in orbit), angular acceleration could only be done by a counter-acceleration, such as with a reaction wheel on satellites. The presence of gravity breaks rotational symmetry and enables offloading angular momentum through a gravitational moment arm. Then angular acceleration is done over many cycles by the relatively limited motion of the body, and the Coriolis effect can be applied to achieve additional tangential acceleration. The mathematical background of the Coriolis effect was discussed in my earlier article on rotating reference frames. The rider gains amplitude by a combination of two methods: reaction moment and Coriolis effect. These differ mechanically in that the reaction moment applies force perpendicular to the line between the pivot and rider center of mass (forward & backward at small amplitude), while the Coriolis effect applies force along this line (up & down at small amplitude).
For a rotating object, moving towards its center of rotation requires work against the centrifugal force, and this work is converted to energy in the form of faster rotation. Overall angular momentum is conserved. However, in a gravitational field, the rider on the swing regularly comes to a stop (or to a slow - this will also work for 360 degree rotations) on either end of the swing cycle. The angular momentum thus is temporarily transferred to the earth-swing system at that point. Returning to a longer radius at this point allows for another bit of work to be done on the next cycle, and so on. To do this, the rider pulls himself closer to the pivot point around the period of fastest swing motion. This coincides with the lowest point of the swing path, so the pull is in the upward direction, meaning the rider is pulling his trajectory upwards and can end at a higher point than he started. The technique is illustrated in the figure below.
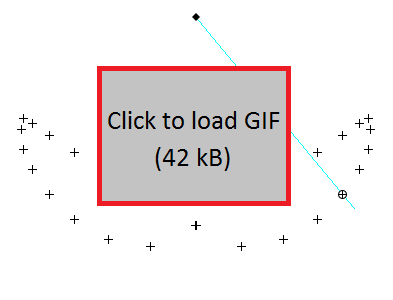
Swing acceleration by the Coriolis effect is achieved by pulling the center of mass towards the pivot point during the faster periods of the swing cycle, and retracting further away from the pivot point during the slower periods. The light blue line represents the chain on the swing, the black diamond is the pivot point, and the circle represents the rider's center of mass. The [+] markers trace out the path of the center of mass over time.
This effect may be simulated by hanging a small weight on a string, passing the string through a hole or over a stationary hanger, then pulling the string at the necessary moments. In this simulation, the string and the experimenter cannot exert any tangential force on the weight, and yet it will be seen to swing higher when the timing is correct. However, for this effect to be appreciable, there is a need to already have some velocity at the bottom of the swing, and this by itself cannot start a stationary rider. Further, from experimenting with a swing set, it seems that one can swing decently well without making use of this effect. At lower amplitudes, a different technique is used which relies on the rider's angular momentum.
An object can generate angular acceleration locally, that is without touching anything, such as done with reaction wheels in satellites. Consider a motor with a heavy disk, attached by a rigid rod to a pivot point. When the motor accelerates, it will generate a moment on the rigid rod, which will attempt to transfer it to the pivot, however as the pivot will not support the moment, instead the entire rod will push the motor tangentially so that its angular momentum becomes the shared angular momentum of the system. Hence the motor and disk will move around the pivot point. The linear acceleration comes from pushing on the pivot point in a direction perpendicular to the long axis of the rod, which is allowed because the rod is rigid. This concept is illustrated below.
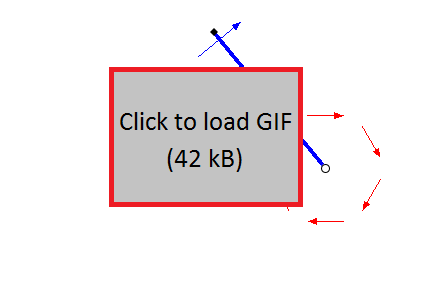
Swing acceleration by the reaction moment, with a hypothetical motorized heavy disk (reaction wheel) on a rigid rod. The black diamond is the pivot point, the thick blue line is a rigid connecting element, the circle is the center of mass. The red arrow hexagon represents the rotation of the heavy disk, while the blue arrow represents the tangential component of force exerted by the rigid rod onto the pivot point due to the acceleration or deceleration of the disk.
However, one does not need to use a reaction wheel when swinging, and from experiments on a swing set, one can accelerate with barely any angular momentum of the body. Further, the symmetric reaction wheel velocity profile above has the highest wheel acceleration at the bottom of the swing cycle, while riding experience suggests that highest angular acceleration of the body is at the ends when the swing is slowest. The rider achieves the moment arm suggested by the reaction wheel above, with only a limited motion of the body, by applying force only for two brief periods at either end of the swing cycle. This is achieved by shifting the center of mass relative to the line of pull, or from the rider's point of view, by exerting a moment on the swing suspension element. With a chain, this would be pulling it behind its nominal position on the forward swing, and pushing it forward of its nominal position on the backward swing. This is further helped by the pull of gravity - because the static force is that of the rider's full weight, a small deviation from the static equilibrium (the center of mass in line with the swing suspension element) provides additional acceleration to the rider.
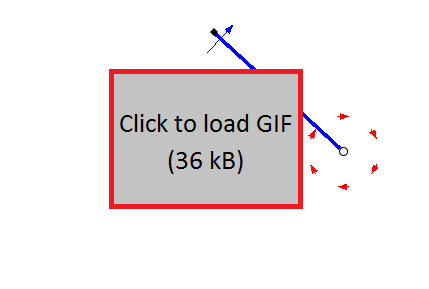
Swing acceleration by the reaction moment, with a more realistic limited range of motion achievable by a rider at either end of the swing cycle. Image elements are defined as in the previous figure.
The work here is done by the rider being pulled upwards at either end of the swing cycle, exerting a moment on the suspension element to do so. In this time, the impact of the moment is just as described in the reaction wheel section, but since the body cannot rotate freely (unlike the wheel), before the next swing cycle starts in earnest there is a counter-moment to slow the body's angular momentum to practically zero. However by now the center of mass is shifted slightly higher, so even though the next swing cycle will not continue to be accelerated by a reaction wheel moment, it will be accelerated by the gravitational offset moment. Typically it is easier for riders to lean far back with arms stretched out and holding the chains, compared to leaning forward the same amount, and in this case the physical work of raising amplitude is done at the forward end of the swing, pulling oneself forward closer to the chains (and pulling the swing bar backwards). In doing so, one is also bringing the center of mass closer to the pivot point, thus shortening the pendulum length, and the swing back doesn't feel particularly fast. It is on the next swing forward that one can lean back (there is not much work to be done here if one did not lean forward very far) and feel the apparently effortless acceleration.
We can again use a model to simulate the reaction moment effect, with a small weight hung on a string and the string held by the fingers of one hand. In the Coriolis model we pulled on the string through a fixed pivot point, while in the present model we will move the pivot point forward and backward at constant vertical height. This sets up forces in the pivot point and string that are similar to what an angular acceleration at the weight would do (but from the other end). The weight is then easily swung to high amplitude even from a zero velocity state. (this is something that crane operators need to have a good intuition about, along with the Coriolis impact possible in lifting a swinging load)
Another analysis is presented here. An important insight from that page is: "At the back of the arc, you throw your head back, but you throw your feet forward. What do these have in common? Both gestures apply a torque to your torso.". However I do not fully agree with the author's approach, because while it is tempting to draw the center of mass offset from the line of pull resulting in a gravitational torque, this is a bit of a "red herring", as in an ideal representation the swing elements would be massless so moving them one way or another won't have an effect. A swing chain may be offset from the line of pull only by means of angular acceleration of the rider (with the rider's arms acting as a rigid element), and it is the moment from this acceleration (rather than shifting the center of mass) which does physical work to increase swing amplitude. Note that if you are leaning back in a swing seat and holding the chains, then releasing the chains constitutes a reduction of muscle effort but is actually a displacement of the chain in principle akin to that if the chains were pulled closer (an increase of muscle effort). Gravity can thus help provide the angular acceleration (without touching anything else, as could a reaction wheel), however this must be countered by a moment force applied by the rider's arms to the suspension element in order to remain seated on the swing, so this effect is ultimately a variation of the reaction moment described above. Reaction moment acceleration does not require gravity; what gravity does for the rider is slow down the swing to zero velocity at either end of the swing cycle, thus allowing the rider to add up angular accelerations about the zero point over many cycles, building up high amplitude without requiring the continuous spinning of a reaction wheel.
Most swings do not use a rigid rod, but rather chains or ropes to suspend the seat. This does not preclude the use of a reaction mechanism, because when the rider uses his arms to hold on to the suspension element, that effectively creates a short rigid segment at the lower end of the swing which can exert a moment through the difference between the direction of force from the pivot to the center of mass and to the suspension element. Further, with the human body, we cannot spin continuously like the reaction wheel, but we can spin for some fraction of a second by changing the body posture. This can be more easily understood by considering a person hanging on a pull-up bar, initially stationary, then beginning a swing and eventually gaining appreciable height; variations on such a move are done routinely in gymnastics and the gymnast need not exert any moment on the pull-up bar with the wrists (indeed doing so would probably lead to injury, in other words the bar may be free to spin about its axis without impacting the gymnast's performance). However the bar is pushed forward or backward (and later down) due to the angular acceleration of the gymnast and the rigid connection of the arms. First, the gymnast would pull up his legs and in the process push back his abdomen and center of mass; the net displacement of the center of mass towards the back is allowed by the simultaneous angular acceleration due to the legs, and is ultimately supported by the pull-up bar being pushed forward by the arms, with the arms here acting like the rigid rod of the earlier example. Next, the angular momentum of the gymnast is allowed to continue and pull him forward, combining with the moment exerted by the displaced center of mass also pulling him forward (toward the bar). Once the center of mass is brought forward of the bar, the legs are brought down, causing a counter-moment on the body with a pulling forward of the bar, and another acceleration of this nature in the reverse. The swing back is completed without substantial further motion due to bodily limitations. On the next swing forward, there is sufficient amplitude that the Coriolis effect can be used to accelerate even further, so at this point the person is a bit slower in pulling the legs back up, engaging in some fraction of both reaction and Coriolis accelerations.
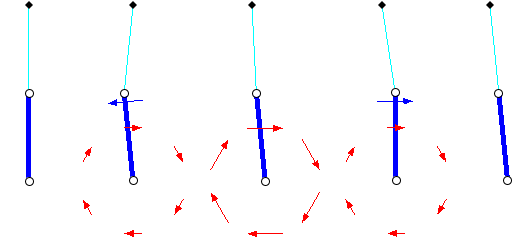
Left to right, snapshots of starting a swing from stationary state with reaction moment. It is possible to start and end with zero angular momentum as illustrated. This can be repeated multiple times to increase or decrease swing amplitude arbitrarily. Image elements are defined as above, with the lower circle representing the center of mass and the intermediate circle representing a pivoting connection between the rigid element (thick blue line) and chain (thin light blue line), and the blue force arrow is the tangential component of force applied by the rigid element to that point.
So on a chain suspended swing, if the arms are used to pull the chain relative to the center of mass, then it is temporarily possible to get some fraction of the force from the pivot to be in the horizontal direction, causing the initial acceleration from a stationary state. From my observations, the technique of pulling or pushing on the chain (offset to center of mass) to generate bodily angular momentum at either end of the swing is most effective for oscillation amplitudes to about 45 degrees off vertical, while pulling downward on the chain at the bottom of the swing becomes more effective at higher amplitudes; in the intermediate period a combination of the two, with a gradual pull that covers some fraction of the swing cycle that shifts from edge to center, seems to be naturally found by the rider. Note that these guidelines are not very strict, and the reaction moment could in principle be applied at any point in the swing cycle while the Coriolis acceleration could be applied during a large fraction of it, so taking into account the constraints and abilities of the body there may be numerous particular bodily motions to begin swinging from a stationary state (similarly, it is possible to decelerate the swing from a high amplitude to a stationary state, even in a frictionless system, by applying these motions in opposite phase).