When the weather conditions are right (scattered clouds and a light haze), looking in the direction of the sun, one may see between the clouds the appearance of rays or beams of light emanating from the sun.

A photograph showing apparent rays emanating from the location of the sun, which is hidden behind clouds. Black lines have been added to aid in identifying the convergence point. The camera does not fully capture the subtle nature of the effect.
The phenomenon seems almost obvious - there is a source of light, and it emits rays outwards, so when small particles in the atmosphere scatter light from the rays, there is an appearance of rays coming out of the object. Yet it is not so simple - since the sun is very far away, its light reaching the earth may be considered nearly collimated (or laser-like in terms of forward propagation, or plane-like in terms of wavefront), thus the outlines of clouds are projected onto the ground along nearly parallel lines through the entire atmosphere. The appearance of these lines converging on the sun is due to a second projection from the 3D volume of the atmosphere to a 2D image seen by the eye, which is the topic of this article.
The projection of geometric rays through a point onto a 2D plane, which is characteristic of photo cameras and of the eyes in a small object limit (eyes are spherical rather than planar), was discussed in my Photogrammetry article. The first steps will be duplicated here: in a 3D Euclidean volume, the lens point is at the origin (0,0,0), and the image plane is parallel to the XY plane passing through z=Di. Then, given a point (x,y,z) we find its 2D image (xi,yi,zi) as follows:
[ xi ] Di [ x ] [ yi ] = -- * [ y ] [ zi ] z [ z ]
zi=Di is enforced, so an image point can be defined by (xi,yi), which represents an object point somewhere along a straight line through the lens point. It is already clear from the formula: as z increases, the projection of a point moves closer to the origin, due to the Di/z term.
With a real lens, focusing may be used to distinguish between nearby and distant objects; since the physical situation here involves large distances (multiple kilometers to the edges of the atmosphere, and much more to the sun) relative to the eye, a real lens would be focused "at infinity", and the single-point lens model will give identical results. (Even with nearby objects, distance is gauged more by the inward turning of the eyes than by differences in focusing the pupil, because the larger distance between the eyes allows for improved angular identification.)
Parallel lines are defined in the 3D volume, then various points are sampled along these lines and projected to the image plane. Different point colors are used so we can distinguish projection distance in the image (a real projection does not carry distance information, which is part of the illusion). The Scilab code for this simulation may be downloaded here.
The image plane is located at Di=-1 and the object points are arranged on a square grid at (x,y)={-1.5, -0.5, 0.5, 1.5} and z={10...100}. The object points are then projected onto the image plane through (0,0,0). The nearer (to the image plane) object points are colored red, while the more distant object points are colored violet, with rainbow colors in between. The code can also simulate angular shifts, but these shifts caused no appreciable difference in the phenomenon, so the scenario presented below is looking straight towards the virtual source.
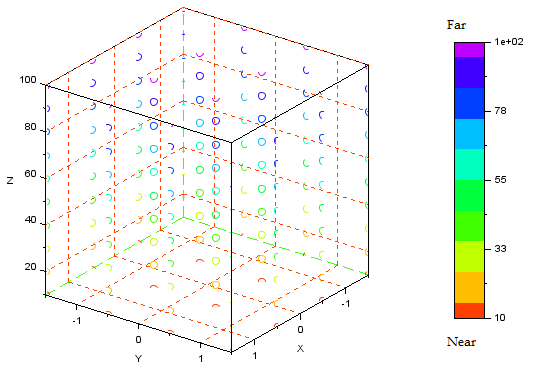
A depth-independent (orthographic) projection of the 3D points onto the figure in this plot shows that they are arranged in parallel lines. Different point colors correspond to different distances along the Z axis.
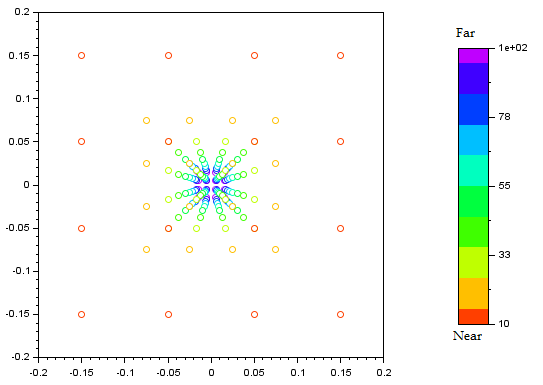
A depth-dependent (perspective) projection of the 3D points onto the image plane in this 2D plot from the point of view of the observer at (0,0,Di) shows that the more distant points in space appear to converge towards a single point in the image plane.
The effect is similar to the convergence of lines when looking down a hallway. The "hallway" in this case is formed by the physically parallel lines of the cloud edges extended through the atmosphere towards the ground, and visually they appear to converge at the "end" of the hallway which points towards the sun. Viewing the phenomenon with this understanding, one can get a better intuition for just how large and distant the clouds really are. Mentally extending a few of the boundary rays' lines until they intersect with the ground, the area encompassed on the ground is the same as the area encompassed by the clouds, since these lines are physically parallel. This is indeed a manifestation of one-point perspective: all parallel lines in the object volume are projected as lines through a single point in the image plane. For sun rays, this single point corresponds with the location of the sun in the image plane, hence the rays appear to converge on the sun, or to emanate from the sun. The closer the rays appear to the sun, the higher up in the atmosphere their light has been scattered from.
There is a similar phenomenon one can observe if standing near a deep and slightly murky body of water on a sunny day, where small particles in the water scatter light that has been focused or dispersed by surface waves, resulting in the appearance of rays extending downwards into the water. Further, these rays appear to converge on a point coinciding with the shadow of the observer in the water (or where the sun would appear if the observer were not blocking it). This seems to be easier to observe when standing on a bridge or other elevated surface with one's shadow extending onto the water below. There is a slight complication in that the refractive index of water causes net bending of the geometric rays when entering and exiting the water volume, however the explanation for the rays' apparent convergence remains the same. As in the atmosphere, the closer the rays appear to the shadow of the observer, the deeper in the water their light has been scattered from (visually closer to convergence point = physically more distant from observer). Despite the increased depth, the rays surrounding the observer's shadow often appear brighter, which could be attributed to retroreflection. (This retroreflection may even be seen on dusty sidewalks and paved roads on a sunny day, as a slight halo around the observer's shadow; it is easiest to make out the halo when moving while looking at the shadow, because the halo remains stationary with respect to the shadow while the road texture moves and appears blurred.)