It may seem a most elementary question: why can't we see stars during the daytime? "Because the skylight from the sun is so much brighter, of course!" Except, in the optical sense, it is not. Stars in the sky are all powered by similar nuclear mechanisms as our closest star (the sun) with similarly high temperatures, and there are very many stars which are hotter than the sun, meaning their blackbody emission spectrum and intensity are more energetic, and hence they are even brighter than the sun. Optical brightness does not change with distance: a streetlight kilometers away looks just as bright as a streetlight a few meters down the road, and the distant light does not become invisible when the nearby light illuminates one's immediate surroundings. So, why aren't the stars visible during the day? And for that matter, why are most stars not visible to the naked eye even at night? This actually has more to do with angular resolution than with brightness.
Let's define observed brightness as the light energy received per solid angle at a detector. For a spherically uniform emitter, such as a star, the solid angle will be proportional to the square of emitter size (star radius R) divided by the distance D to the emitter (θ ∝ R2/D2). The amount of energy from the emitter E reaching the detector will be proportional to the generated energy G divided by the squared distance from detector to emitter (E ∝ G/D2). Then the observed brightness is B = E/θ ∝ G/R2, which is independent of emitter distance. Thus, the fact that the sun is nearby and other stars are far away, does not mean that the sun is brighter than other stars, and many brighter stars exist with higher generated energy G (hotter temperature), smaller radius R, or both. However, viewed from the earth, the solid angle subtended by distant stars becomes increasingly tiny, while that from the sun is large. We can illustrate this schematically.
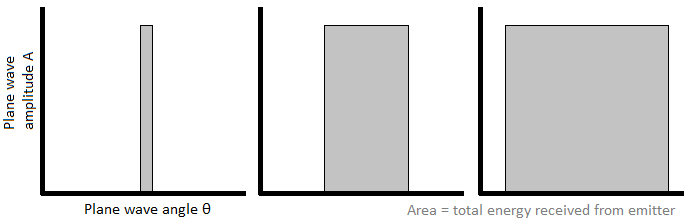
This image illustrates the light received from three objects, which will appear equally bright. On the left, an emitter that appears small (a distant streetlight) delivers less total energy to the detector, but at a narrow range of angles. On the right, an emitter that appears large (a nearby streetlight) delivers more total energy to the detector, but over a broad range of angles. Dividing total energy by angle range leads to a constant brightness for all these objects. If an aperture, such as a piece of black paper with a hole in it, is used to limit the observed angular range of (and total energy received from) the nearby emitter, the part of the emitter that remains visible will look just as bright as it did before. Moving further from the emitter reduces the range of angles that reach the detector, but does not reduce the amplitude of plane waves in this mathematical representation, so brightness is again unchanged.
Then we have the influence of skylight, which is relatively quite dim, but covers a very wide range of angles. Skylight comes from scattered starlight, and as we barely see any skylight at night, we conclude that even though the skylight during the day is bright, it is still only a fraction of the brightness of the original source which is sunlight. Light coming from distant stars is just as capable of being scattered by the atmosphere as light from the sun - in a long enough exposure of the night sky we will see blue skylight originating from the stars. Namely, as we see the sun during the day with no difficulty, and see the stars during the night with no difficulty, it should not be a difficulty to see the stars during the day because the skylight is of low relative brightness. This must be so because skylight comes from a wide range of angles but carries the same energy as was originally in a narrow range received from the source star, so its brightness is reduced accordingly (and substantially). However, any detector we make will have a physical size with associated limitations on the minimum range of angles that can be differentiated as a single pixel (to include diffraction effects). There is, so to speak, a "bucket" that will collect all the energy within a range of angles, and this range will be much larger than any individual star, because stars are very far away. Even with high power telescopes, the range of angles received from an observed star will be smaller than the responsivity of a detector pixel, so any star, if it is seen at all, will be seen as a single pixel (plus diffraction effects) despite its true image being smaller yet.
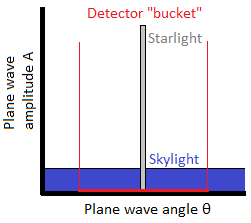
Shown is a schematic comparison of optical brightness from a bright star (gray) and dim background skylight (blue), incident on a detector "bucket" (red) that captures all energy over some range of angles defined by the optical hardware. As the detector intrinsically carries out an integration over its acceptance angle range, the total energy from the skylight overwhelms the total energy from the star, even though the latter is much brighter (more concentrated).
In other words, the angular resolving power of all practical telescopes is insufficient to tell apart stars from skylight. This is true for the eye as well, which is why the stars are invisible in daylight. Another aspect of detector design applies - it is easy to tell apart small differences in energy when the total energy is near zero, so for instance it is easier to tell apart 0 from 1, as opposed to 10000 from 10001 units of energy on a detector. If the energy incident from a star is 1, and from skylight 10000, then even though by energy conservation it could be visible in daylight, practically our detectors cannot achieve such exact and low-noise energy discrimination (more critically, the sensitivity to sunlight energy and atmospheric conditions is accordingly higher than sensitivity to desired starlight). There is another detector limitation, which is the minimum amount of incident energy that it can respond to (to transition from 0 to 1, so to speak). If we improve angular resolution, we still have to contend with the fact that only a small total amount of energy from distant emitters will reach the detector. If this total amount is too small, we will only see a "black spot". This in turn is why most stars are invisible to the naked eye - the total amount of energy delivered in a tiny angular range is not enough to fully activate a particular "bucket" on the detector (light-activated chemical reaction in the eye's photosensitive cells). The total energy is increased by the use of binoculars with a large front lens, so more stars are visible then (the angular size of stars is also increased by binoculars, however this size is so far below the minimum angular discrimination of the eye that this makes no difference to perceived image formation; the optical brightness of the star remains unchanged or perhaps is decreased). To make faint stars visible, very long photograph exposure times are used even with the most powerful telescopes, which increases the total amount of energy integrated by the "bucket" beyond the necessary threshold. The need to use long exposure times means that a true image of the stars being made visible would be substantially smaller than one "pixel" of the instrument.
Still, with all these reasons why stars should not be visible in the day, it remains true that their brightness is high - so with great care they should in principle be visible. From this page we quote: "[Y]our eye has difficulty focusing to infinity when you are looking at a featureless blue sky. If you are trying to see small, faint things like stars it is critical that your eye be focused precisely. However, if you look at a blue sky there is no reference object for your eye to focus on and it is difficult to correctly focus on a star. Nevertheless, it is possible to see some stars in daylight. The stars must be bright, such as Sirius, Arcturus, Vega, Capella, Rigel, etc. You also need to know exactly where to look, in advance. Finally, it helps if there is some very distant object right next to the star that you can focus your vision on. Aldebaran is a good star to try to see because it lies near the plane of the ecliptic, and the moon passes very near it once every 28 days.". And Colin Henshaw's "On the Visibility of Sirius in Daylight" (Journal of the British Astronomical Association 94/5, 1984) is an academic source on the veracity of seeing this star shortly before sunset or after sunrise (along with other stars at midday through a telescope).