Clouds can be seen almost every day, on clear days even extending far towards the horizon. It is difficult to judge cloud size since clouds are far away and have no clear identifying features. With help of a simple geometrical model, and an idea of the cloud height above ground, it is possible to estimate cloud size based on the extent of sky solid angle the cloud appears to take up. To measure this angle it is possible to make a simple device using a string with markers or a printed image.
The horizon is defined as the farthest point of land (at sea level) visible from a typical human height, standing at sea level. This point is farthest because of the curvature of the earth (light refraction is not taken into account). To find this point, I use these values: typical human height h = 1.65 m, earth radius Re = 6.371e6 m. Because of the orders of magnitude difference between the earth radius and any of the other heights used in this article, it is acceptable to use an approximation that the horizon is at exactly 90 degrees. I compute the values numerically with a full model that takes the curvature into account, but the results of this model are almost indistinguishable from the approximations (code download). To make all calculations consistent, I will define view angle theta as the angle from the vertical line (local gravity 'down' direction) such that 0 means looking straight down, and 180 means looking straight up. The horizon then is very close to 90 degrees, and the region 0-90 is taken up by ground, while in the 90-180 range clouds are seen.
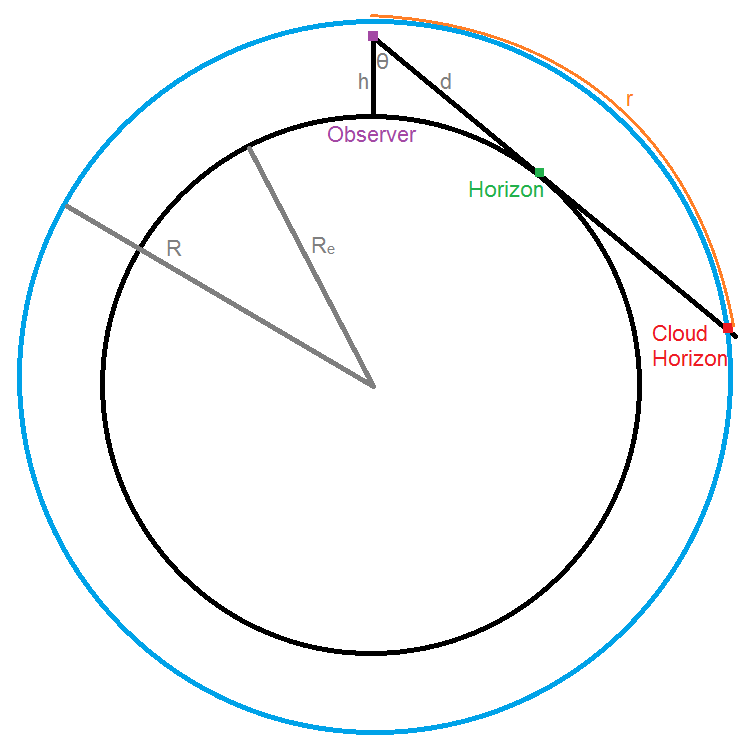
Variables used in the analysis are shown above: Re, earth radius (6.371e6 m); R, cloud radius; h, observer height (1.65 m); d, distance from observer to object in sky; theta, view angle from downward vertical; r, size of cloud extending from a particular theta to directly overhead.
The horizon is found to be at a view angle (theta) of 89.96 degrees and at distance of 4585 meters (compared to 90 degrees and infinity for an infinite plane). Tall buildings or hills can be seen much farther than this ground horizon (skyscrapers can be seen from well over 20 km even at ground level, contributing to the 'surreal' experience when approaching a big city). The horizon can also be extended if the observer is higher than ground level. The rise of distance with view angle is very steep – most of the distance to the horizon is covered within only a few degrees. Note the almost vertical slope when approaching the horizon in the following plot of distance as a function of view angle.
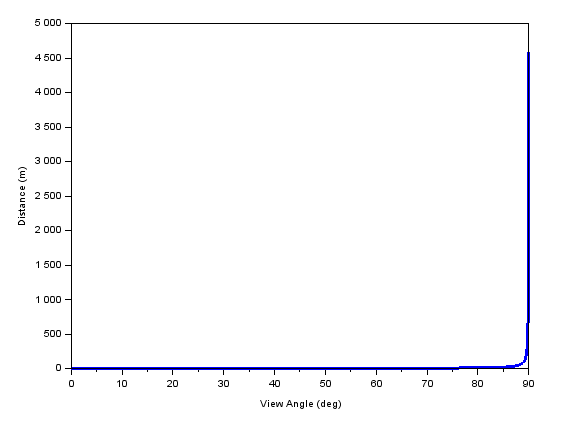
Distance from observer to ground objects (all at sea level) which are seen at a given view angle.
A few points from this curve are tabulated below. Exceeding just 100 m takes over 89 degrees, which leaves less than 1 degree for the remaining 4485 m.
| View Angle (deg) | Distanced (m) |
| 0.000 | 1.65 |
| 75.494 | 6.59 |
| 82.629 | 12.9 |
| 85.071 | 19.2 |
| 86.299 | 25.6 |
| 87.038 | 31.9 |
| 87.531 | 38.3 |
| 87.883 | 44.7 |
| 88.147 | 51.0 |
| 89.011 | 95.7 |
| 89.505 | 191 |
| 89.751 | 383 |
| 89.854 | 663 |
| 89.901 | 995 |
| 89.937 | 1709 |
| 89.950 | 2417 |
| 89.956 | 3106 |
| 89.958 | 3807 |
| 89.959 | 4585 |
So, about 90% of the distance (458 to 4585 meters) to the horizon can only be seen within 0.2 degrees of the horizon line. For reference, the width of a finger held at arms’ length covers approximately 1.5 degrees in the field of view. The distance to the point at 1.5 degrees below the horizon is a tiny 57 m, meaning 98.7% of the distance to the horizon is to be seen within a finger’s width of the horizon, and most of that distance in turn is covered in the 1/8 of finger width closest to horizon line. So the vast majority of what we see (based on the view angle) is determined by very close surroundings – about 100 meters. After that, the farther objects tend to all blend into a tiny slice of the field of view. While we can see bright lights out to the horizon (ideally), it takes an effort to make out shapes or features beyond about a hundred meters. This is why we lose track of far away planes or ships. Considering the earth radius of 6371 km, looking at the horizon around oneself puts in sight about 1.3e-7 (or 0.000013%) of the earth’s total surface area.
I considered the ground first, because that sets the lowest view angle for the sky (at the horizon). The sky can be viewed at any angle from the horizon (89.96 deg) to directly upwards (180 deg). Clouds are typically divided into three categories: low height (0.2 to 2 km), medium height (2 to 7 km), and high height (5 to 14 km). For simplicity I use only a single height for each level: 1 km, 4.5 km, and 10 km. 10 km is also the cruising height of a typical airliner (30000 ft). What is the distance from observer to cloud when looking along a given view angle? This is presented in the plot below, for the three considered cloud levels. Unlike the relatively modest ground horizon at 4.6 km, the 'cloud horizon' for the highest clouds is an impressive 361.7 km, and even for low clouds exceeds 100 km. This is the same mechanism by which tall structures can be seen from much farther away than the ground horizon, as mentioned above. (code download)
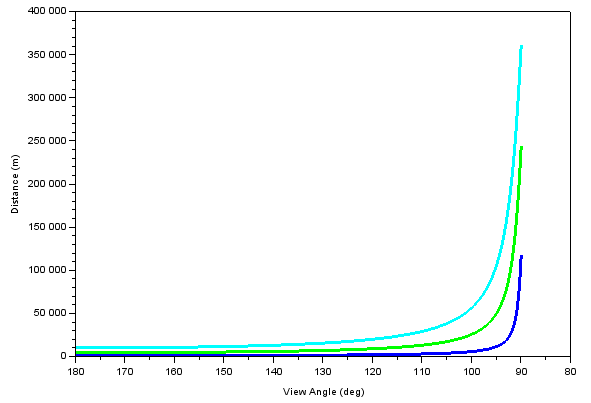
Distance from observer to clouds which are seen at a given view angle. Dark blue = 1 km high clouds, green = 4.5 km high clouds, light blue = 10 km high clouds/airplanes.
How big are the clouds that we see? I approach this by finding the effective radius r of an imaginary circle for a given view angle (by ‘effective’ I mean adjusted for the slight curvature of sky and not a straight-line radius, though this adjustment is smaller than a few parts per thousand). Looking straight up (180 deg), the radius is zero. Looking within a cone with edges at a given angle from vertical, the radius is based on how high up the clouds are. For instance, if a cloud fits entirely within the 170 deg view cone, then its length is twice this radius. Looking towards the horizon (90 deg) the radius will approach the distance from eye to cloud but will be larger. This radius is plotted as a function of view angle for the same three cloud heights as above.

Radius of virtual circle drawn at a given view angle and height. Dark blue = 1 km high clouds, green = 4.5 km high clouds, light blue = 10 km high clouds/airplanes.
This is quite similar to the earlier distance plot, except now the starting point is zero radius when looking directly up, and eventually approaching values very close to the observer-cloud distance at low view angles. Both of the above plots are tabulated below as a function of view angle, where we see that once again the largest increases in both d and r occur within a few degrees of the horizon.
| View Angle (deg) | low cloudsd (m) | low cloudsr (m) | med cloudsd (m) | med cloudsr (m) | high cloudsd (m) | high cloudsr (m) |
| 180 | 998 | 0 | 4498 | 0 | 9998 | 0 |
| 175 | 1002 | 85 | 4514 | 379 | 10036 | 866 |
| 170 | 1013 | 176 | 4565 | 784 | 10152 | 1764 |
| 160 | 1062 | 362 | 4782 | 1623 | 10634 | 3623 |
| 150 | 1153 | 578 | 5194 | 2597 | 11542 | 5772 |
| 140 | 1304 | 838 | 5879 | 3787 | 13050 | 8431 |
| 130 | 1554 | 1190 | 6993 | 5355 | 15577 | 11954 |
| 120 | 2000 | 1733 | 9019 | 7820 | 20046 | 17388 |
| 110 | 2916 | 2740 | 13017 | 12219 | 28930 | 27168 |
| 100 | 5732 | 5645 | 25562 | 25172 | 55919 | 55061 |
| 95 | 11332 | 11289 | 49310 | 49122 | 104721 | 104326 |
| 89.96 | 117470 | 117477 | 244083 | 244143 | 361687 | 361881 |
So far, I have referred to view angle theta as a primary variable to find out the size and distance of objects. But this is not intuitive – while our eyes measure the angular aspects of incoming light, we do not have a great idea of what a 10 degree light cone might look like because we are used to judging actual object sizes rather than their perceived angular sizes. A car in the distance will seem to be 'just as big' as a car up close, even though the angle taken up by the distant car could be less than half of that taken up by the nearby one! Thinking in terms of perceived angular size is something artists have to practice for realistic perspective drawings.
Is there a way to tell, in a practical setting, what is the observer’s current view angle? It is possible to use instruments such as a sextant to measure the perceived angular dimensions accurately, but a simpler approach is also available to get a quick representation of how much of the sky a given view angle covers. This involves having a string/rod with markers along its length, oriented at 45 degrees to the vertical line (ground normal). Then the observer is situated such that looking at the horizon means looking towards one end of the string, while looking directly up means looking towards the other end of the string. There is only one such point, which forms an isosceles right triangle with the string as the hypotenuse. From this point, if markers on the string are positioned at specific locations, looking towards one of the markers will mean looking at a specific view angle. Having the markers far away from the observer will make this setup less prone to errors from slight movement of the observer from the 'ideal' location.
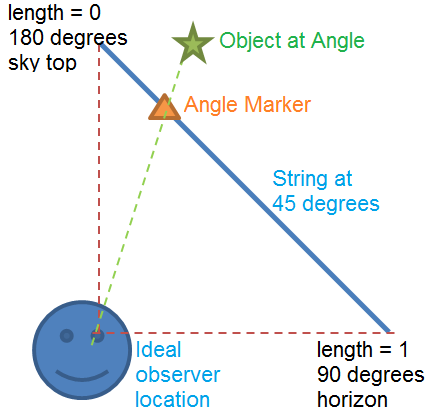
Layout for the string method of measuring view angle of objects in the sky.
The locations of the markers, measured along the length of the string (normalized to 1), as a function of view angle, are tabulated below. (excel download)
| View Angle (deg) | Length (rel) |
| 180 | 0.000 |
| 175 | 0.080 |
| 170 | 0.150 |
| 160 | 0.267 |
| 150 | 0.366 |
| 140 | 0.456 |
| 130 | 0.544 |
| 120 | 0.634 |
| 110 | 0.733 |
| 100 | 0.850 |
| 95 | 0.920 |
| 90 | 1.000 |
It is also possible to use a paper print-out, or even a computer monitor for this purpose. Then, one of the long edges of the paper acts as the 'string' and has marks equivalent to the above table. The second dimension of the paper also needs to have a projected circle appearance. For this a projection script was written, which assumes the paper is held at 45 degrees such that looking up means looking at one corner and looking at the horizon means looking at a short edge touching the ground. The long edge of the paper should form the 45 degree line, and the topmost edge of that line should be in the center of the field of vision when looking directly up (180 deg view angle). When properly oriented, the outlines on the paper will appear to the observer as expanding circles centered on the paper corner point (180 deg). Since a printed page will be small and close to the observer, this effect will require looking at the tilted image with only one eye. The image shows view angle lines corresponding to the above table. Bottom left corner is the 180 deg point. Right edge is the horizon line. Bottom and top (long) edges should be oriented at 45 degrees to the ground.
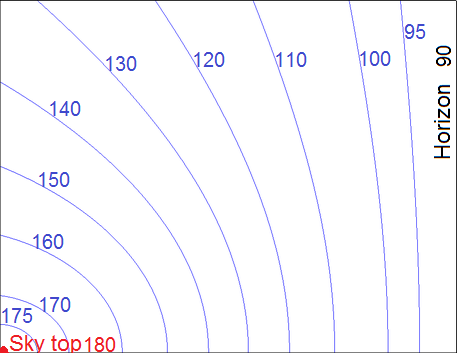
2D projection of view angle, assuming a printout of the image is held with the long edge at 45 degrees to vertical, similar to the string-based concept above. The image aspect ratio is chosen for letter size paper (8.5x11 inches). Angles corresponding to each line are shown, a larger version without labels for printing is linked.
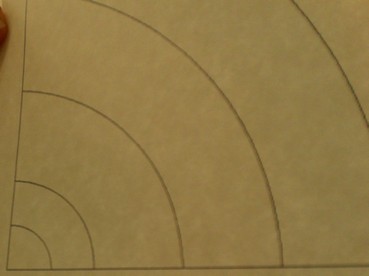
When the above image is printed and oriented as described with respect to the observer, the lines appear to trace out concentric circles, each at the given view angle. The printout will cover 1/4 of the sky area, and the lines can be mentally extended to the open area to determine the angles at which different clouds are seen.

Side view of how the image can be used to determine the 'view cone' angle.