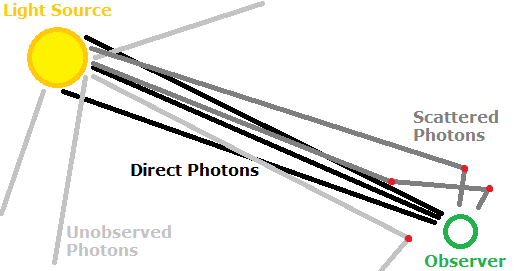
A photon transport representation of skylight as scattered direct sunlight.
The appearance of the sky, as well as of distant objects near the horizon, can be understood with a theory of photon transport, which extends beyond classical optics. Its similarity to particle transport as studied in other physics fields (such as neutron transport) allows us to make some simplifying assumptions and still understand the reasons behind the appearance of objects.
To begin, the idea behind basic photon transport is described. A photon is taken to be a particle-like entity, which is created at a certain origin position in space, a frequency, and an origin orientation vector in which the photon travels, at a constant speed c, the speed of light. In vacuum (in absence of interactions) this photon proceeds along the straight line path described by its velocity vector in space, and if along its path it is incident on some matter (air/water molecules, solids, etc) it will interact with the matter. The interaction may absorb the photon or it may change the velocity vector direction while keeping frequency constant (Rayleigh or Thomson scattering). This model also allows for the change of photon frequency, creation of other photons, and other non-linear effects not handled by classical optics. Since these non-linear effects are usually rare, they will not be considered here, as scattering and absorption are sufficient for a general understanding. Further, we clarify the function of the eye as a mechanism by which the incoming direction, frequency, and time of incidence of a photon is acquired. It should be noted that the 'depth' or distance which a single photon has traveled is not measured by the eye and such observations are made by assuming multiple photons originate at the same point, an effect that allows 3D and holographic displays to function.

A photon transport representation of skylight as scattered direct sunlight.
We know that at night, stars are seen clearly which suggests the sky is transparent, while during the day the sky becomes an opaque white-blue color which prevents stars from being seen. By saying that the stars are visible at night, we mean that photons originating from those stars largely maintain their travel direction (velocity vector points from star to earth) until being incident on the eye, which allows the identification of the star as a photon source at a particular point in space. Furthermore, it is implied that there are few photons with velocity vectors close to those of the star (from observer's viewpoint), meaning the area surrounding the star is dark which allows the differentiation between the star and 'empty space'. This means that when one is looking at a particular star, all the observed photons actually originate at the star and travel in an essentially straight path from their last collision in the star directly to the observer. If this were not the case, say if there is a dust cloud between the star and earth that scatters incident photons, there would be no method by which the observer could identify the original velocity vector (and thus location in space) of the photon origin. A dust cloud giving off light could be illuminated by any incident photons, thus only a general glow will be observed. If matter is taken to be very dense dust, it is seen that a very similar effect occurs with opaque objects such as a sheet of paper or a painted wall. Photons incident on such an object may be scattered in any direction that does not travel into the object, thus all spatial information of incident light is lost. This is the main distinction between a white object and a mirror, both of which can be made to reflect photons very effectively.
Now that the general ideas of photon transport are established, we consider the appearance of the daytime sky. Clearly, to observe the blue color of the sky, photons must be incident on the observer with velocity vectors corresponding to all positions in the sky. These photons greatly outnumber those originating from the stars, and make the stars impossible to see in daylight. We reason that, since the sky is transparent at night, the photons that give the sky its blue color must originate from the sun. Thus these photons are generated at the sun, and yet are clearly observed to arrive from all directions in the sky rather than the sun's actual position in space. Here the paper sheet analogy may be useful. While the sun appears to be a small disc (with an apparent size close to that of the moon), logically it illuminates an entire half of the earth's spherical surface, and thus photons are incident onto the atmosphere across the surface of the earth. Particles in the air, as well as air itself, can scatter light, albeit very slightly since earth objects on a human vision scale are always clearly visible in air. However photons from the sun have to traverse the entire thickness of the earth's atmosphere before being incident onto any matter, and through this large distance the air behaves visually like holding up a thin paper sheet between a light bulb and the observation point. That is, a significant number of photons continue on their straight path from the sun to the observer, which gives the appearance of the very bright solar disc, while other photons are scattered from their straight-line paths at every point within the atmosphere, leading to a uniform source of photons that are a source of the sky's observed brightness. Of course the total number of photons is conserved (or at least not increased) so the sun appears significantly brighter in space than on earth's surface. Photons originating from the stars will also logically be scattered, however the brightness of the sky (number of photons considered skylight) is proportional to the brightness of the star (number of photons considered to originate from the star). Since the sun is much brighter than other stars (due to its proximity), the skylight due to the sun completely outweighs the directly incident photons of the stars, making them impossible to observe during the day. Also since the atmosphere's scattering is low enough that we are able to see multiple stars at night, it is logical that if there were more suns in our planetary system they would be visible during the day (many suns may be an unlikely idea, but sunlight reflected off the moon certainly is visible during the day).
With the origin of the skylight photons explained, it is necessary to consider the sky's color. The color is caused by differences in the probability of scattering of different frequency photons. Avoiding excessive complication, it is adequate to say that high frequency (blue) photons are scattered more than low frequency (red) photons, so to an incoming blue photon the atmosphere appears 'thicker' or more diffuse than it does to a red photon. Then the skylight, which is defined to be entirely scattered photons, will be biased towards the blue color photons, while nonetheless containing the other colors, leading to the sky's blue-white (or light blue) appearance. On the other hand, the sun will appear more red than it would in space due to some blue photons being scattered from the direct path. During the sunset, the sun direct-path photons have to travel through more air than when the sun is directly overhead, and thus the sun appears redder. The sun's temperature and blackbody spectrum, as well as the eye's frequency response, cause blue to be the dominant sky color (in theory, the higher-frequency violet has a higher scattering probability in the atmosphere than blue, but there are less violet photons incident on the earth than blue photons and the eye is less responsive to them).
The appearance of earth objects at distances nearing the horizon arise from the same photon transport phenomena described above, but for better understanding a more detailed treatment is necessary. First, we specify that scattering can occur only due to individual particles with which a photon interacts. In air there are many varieties of such particles, each of which has different interactions with photons, but when considering the atmosphere as a whole we assume that an imaginary 'conglomerate' particle type can describe all interactions. Then, when a photon hits this particle, it will interact and possibly scatter or be absorbed (assume no other reactions). For a photon to hit a particle, there is a geometric factor of the particle size and its concentration in air, namely the cross sectional area of all particles suspended in air as seen by the photon, or simply the cross-section (note that this is not a physically measurable area but an imaginary measurement). The larger the particle, and the more particles there are per unit volume of air, the higher the chance for a photon to interact. Also depending on particle type and photon frequency, the interaction probability may change, but since we do not desire so much detail all of these are assumed to be approximately constant and are then grouped into the cross-section measurement. Second, we ignore absorption and assume scattering is the only allowed reaction. Furthermore as justified above, we ignore frequency effects and assume that as long as the photon hits the imaginary particle, it will always scatter in a random direction. By adjusting the imaginary particle size we include the probability of scatter in the calculation, while particle concentration should be proportional to air density as well as actual particulate matter in the air (fog, smoke). Third, we assume a small photon size in relation to imaginary particle size, meaning the only effect on scattering will be the geometric cross-section of these particles.
Since a photon does not have a history in this model (that is, its probability of scatter is not affected by past scatters), its probability of scatter is always constant for an infinitesimal travel distance as long as air properties are uniform so probability of scatter while traveling from distance 0 to dx is p(dx)=u*dx where a is constant. To scatter in the next dx interval, the photon must not have scattered in the original dx, so dx must be small for this formula to hold. Integrating the differential equation gives the probability of scatter while traveling a large distance from 0 to x, P(x)=1-e^(-ux). The limit of P(x) is 1 as x increases, so in an infinitely long channel every photon will scatter when there is a nonzero scatter probability, which is logical.
The magnitude of u is based on the density and amount of particulate matter in the air, thus changing constantly, and takes work to determine experimentally. For now, we simply assume u is constant, and at the end of this analysis ideas for determining u will be presented. Meanwhile the exponential relation is a significant finding. To better understand what this implies for observing objects near the horizon, a simple diagram is constructed.
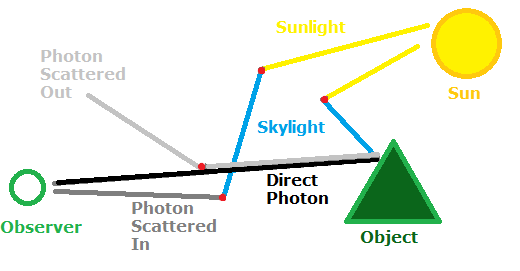
Visual representation of the possible photon paths when observing an object illuminated by skylight.
A few assumptions are made here: first, the observer distinguishes the direction of incoming photons (retina accomplishes this) and collects photons over a small geometric area (the eye's pupil is a very small collection area compared to large distances considered here). This means that if photons are observed to come from a particular direction, they either originated at an object and traveled in a straight line towards the observer, or they originated elsewhere and have scattered onto a path towards the observer after interacting with a particle in air along the straight-line photon path. Second, we assume all photons are of the same frequency, so the observer cannot distinguish between scattered and direct photons if they appear to originate at the same point, and so that interactions in air are the same (and occur with the same probability) for both photon types. Third, the photon source of all visible photons is taken to be the sun, and the photon path from object to observer is nearly horizontal so that air density and ambient light intensity is constant along the path.
Then when an observer looks at an object, photons which have scattered or reflected off the object have to traverse the entire length of the straight-path line from object to observer without scattering along the way (the small observation area assumption allows ignoring photons that scatter out and then back in). In other words, for a photon traveling towards the observer a single scatter event is understood to make that photon unobservable. Then as derived above, the number of unscattered photons from an origin point arriving to the observer is 1-P(x)=e^(-ux). This means the object's apparent brightness is attenuated exponentially (brightness as used here already takes into account the geometric factor of the object simply being further away but also appearing smaller in proportion) and an object that is very far away in air will become invisible since very few photons from the object will arrive to the observer without a single scatter event. This would be the situation at nighttime, when far away lights would tend to become invisible if air scatters heavily (such as in fog). During the day, however, the ambient skylight and sunlight provide a constant source of photons incident on the straight-line path which have a chance to scatter towards the observer. As the path is taken to be horizontal, and ambient light to be constant, there should be a constant number of photons scattered onto the path for each distance increment, that is the total number of photons scattered in is proportional to the path length. Also the scattered-in photons will be generated with uniform probability anywhere along the path length.
In formulaic terms, we assume that O photons are reflected or scattered from the object towards the observer (refer to as direct photons). Of these O photons, only e^(-uD) will arrive at the observer, with D being the distance between the observer and object. Meanwhile, there will be A*dx photons per unit length incident onto the direct path from ambient light, and with scatter probability u there will be a total of AuD photons scattered in along the path. The scattered-in photons are subject to the same possibility of subsequent scattering out, so with a uniform generation rate the number of photons arriving is the integral int{0,D}(Au*e^(-ux)*dx) = A*(1-e^(-uD)). In the case that the object does not generate its own light, the magnitude of O is based on ambient light sources. When the object is illuminated by sunlight directly, it is expected that O>A, while if it is illuminated only by skylight, O<A due to photon absorption, and in case of a perfect reflector of skylight O=A.
For an object to be visible, the number of photons arriving from the object needs to be sufficiently different from the number of photons arriving from ambient skylight. The total number of photons seen by the observer is S=O*e^(-uD)+A*(1-e^(-uD))=A+(O-A)*e^(-uD). When O>A, the object will appear brighter than the sky, O<A the object will appear darker, and O=A the object will be invisible. The number of photons observed when looking at the sky will correspond to O=0 and D=very large (assume infinity), so e^(-uD)~0 and S=A. Similarly when the object is perfectly reflective O=A and thus S=A for any distance. We see that for nonzero scatter probability u, any object that is taken far enough away from the observer will blend in with the sky, as a consequence of its photons scattering out and skylight photons scattering in. It is generally easier to find objects on the horizon illuminated by skylight rather than direct sunlight, thus we expect that when nearby objects are darker than the sky, farther away objects will become lighter until they blend in with the skylight color and brightness. A few photographs from an image search of 'horizon mountains' verifies this effect.




Four examples of mountains illuminated by skylight extending towards the horizon. In each case, the nearest mountains appear dark (due to their low reflectivity of the incident skylight), but the farthest mountains appear lighter, eventually approaching the color and brightness of the sky. This is due to skylight photons scattering into the straight line path between the observer and the mountains.
Like the magnitude of u, the threshold at which objects become visible is a parameter that is difficult to determine. But it is reasonable to assume that under similar lighting conditions (magnitudes of A and O), this threshold will be approximately constant for the same observer. Then, experimentally determining which objects are visible from a particular point can be used to track changes in other parameters based on whether those same objects are visible under different conditions. With the further assumption that the visibility threshold (ratio between photons from object and photons from sky for object to be visible) is independent of the overall illumination brightness A, and that the observed object always reflects a constant fraction of the illumination O=nA where n is a property of the object (how reflective it is). Then for an object to be visible at threshold T = S_o/S_s = (A+A(n-1)*e^(-uD))/A = 1+(n-1)*e^(-uD) is a constant. D and n are also constant for the same object and observation point, so observing which objects are visible at a certain distance D is a way of measuring u. If over time closer objects become invisible or farther objects become visible, it is possible to measure changes in u without knowing the absolute magnitude. Specifically, for a doubling of visibility distance D, there is a halving of scattering probability u. This can be put to use in measuring concentration of particles in air, such as pollution. In this case the increase is assumed to be solely due to high volumetric concentration of strongly scattering particles, which is taken to have a proportional effect on u via the geometric particle area interpretation. With a proper scaling factor on u the farthest distance to visible objects in daylight should serve as an inverse measure of density of particles suspended in air (may be pollution, fog, snow, etc). The photos below taken in Beijing (AQI of 300, ....) show that far away objects become invisible as the pollution index (scattering probability) increases. It is almost metaphorical that the exponential nature of scattering only affects long distances, while nearby objects still appear effectively the same (just like we keep polluting the environment and not worrying about the effects because the only thing we observe directly is short-term changes which are relatively benign).



Beijing on a clear day (AQI ~20).



Beijing on a more polluted day (AQI ~100).



Beijing on a very polluted day (AQI ~300).