Why do shadows sometimes appear clear and sometimes quite blurry?
Let's define shadow quality as the measure of the 'fuzzy area' surrounding a shadow, that is where there is clearly less light than if the shadow-casting object was not present, but yet more light than is present in the full shadow of this object. Then a smaller blurry area means a higher quality shadow.
From this definition we see that a clear shadow requires a clear relationship between the object's shape and how it affects the field of light around it. Unlike general fields, photons cannot spin or be scattered without hitting an object, and thus can be assumed to travel in straight lines from their source to their destination. That means for a general shadow, in order to reduce the blurry area there must be a clear criteria of whether the object's edge is blocking the light or not. This leads directly to the light's source.
Mathematically, a one-to-one correspondence is requested between the object's contour and its shadow edge in terms of photons striking both. Due to the straight-line nature of photon travel, having such a correspondence requires either a collimated light source (where all photons travel in parallel lines) or a point light source (or an appropriately divided combination of both). This is also possible with a focused light source (an inverted point source of sorts), but realistically, a near-point source is a much more common occurrence than a collimated source, since any object appears to look like a point if viewed at a sufficient distance (such as stars).
Therefore in general a high quality shadow can be achieved if (since in both of these cases a one-to-one mapping is approached)
Conversely, the shadow quality can be used as a measure of how close the light source is to a point source. Taking simple solar shadows as an example, we see that the sun is a poor point source even if it is too bright to look at directly. (Note that the blurriness of sun's shadows has been attributed in some physics classes (!) to be caused by the diffraction of light, or its uncollimated nature, or its non-monochromatic nature. All of these effects are present but are greatly outweighed by the fact that the sun is round and thus each shadow edge will have a corresponding round disc around it causing the blur. By greatly outweighed I mean that diffraction of light in shadows should only be relevant for distances appropriate for microscope measurements.).
Additionally, with a non-point source, shadow quality can be used to determine the object's height above the shadow surface. Thus under streetlamps of a uniform height, tall trees will cast a worse quality shadow than short trees. On a sunny day, objects closer to the ground will have a much clearer shadow - planes flying low to the ground may cast a shadow while planes flying at a high altitude will not (from the ground, a plane flying low will appear to cover a significant fraction of the sun while a plane flying high will not).
We test out the above analysis with a few experiments. To confirm the idea of a point or collimated light source requirement, we image the same object (a plant) with a fluorescent bulb (fairly big light source), an LED (almost a point light source), and a laser diode (very close to a point source). As expected, an increase in shadow quality is seen when all the distances are kept constant.



Left to right, the plant's shadow is made with a fluorescent bulb, an LED, and a green laser diode. As the light source becomes more point-like, the shadow quality improves.
To compare between the LED and Diode Laser shadows, close-up images were also taken:

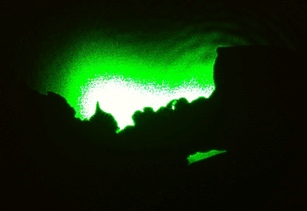
Close up zoom of the LED and Laser shadow edges, which shows the laser gives a much better shadow.
Next we test the distance hypothesis, that objects closest to the shadow plane appear clearer than objects far away. For this an antenna rising towards a ceiling is illuminated from below when the photograph is taken. This is done with the fluorescent and the LED bulbs. For the fluorescent light we see a clear effect of distance, as the tip of the antenna casts a clean shadow while the base (being far from the ceiling) casts a blurry one. This is what the shadow of a tree in the sun might look like. For the LED, however, there is no visible effect of object distance because the LED is a much better point source.
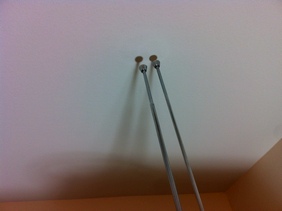

Antenna shadow with a fluorescent bulb (left) and LED bulb (right).
The above analysis can be seen to apply to optics in general. For images in a camera, the focus of a projection is a measure of the one-to-one mapping of physical object edge with optical sensor location. The lens in a camera may allow focusing, which sets the distance at which the camera assumes photons originate. A focus lens thus effectively creates a point source from a non-point source by using the distance as a parameter. Increasing the aperture, or decreasing the area through which photons can pass to the limit of a single point, necessarily creates a one-to-one correspondence and will thus bring all parts of an image into focus but will also block many photons from ever reaching the sensor. Decreasing the aperture on the other hand will let in more photons (useful for practical camera considerations) but will increase the blur of objects that are not at the distance specified by the focus of the lens.
Microscopes are even more dependent on a one-to-one correspondence since they deal with small distances and small angular displacements. For this reason, microscope lenses tend to be expensive precision instruments.