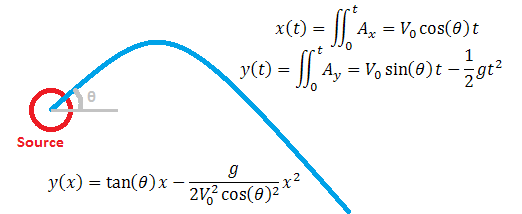Ballistic Problem
July 6, 2015
Introduction
This problem is an exercise in finding an optimal trajectory for a ballistic launch (throwing something). For example, consider water coming out from a garden hose - the question is, how should the hose be aimed so that the water lands the farthest away from the source? A related question is what that longest distance will be.
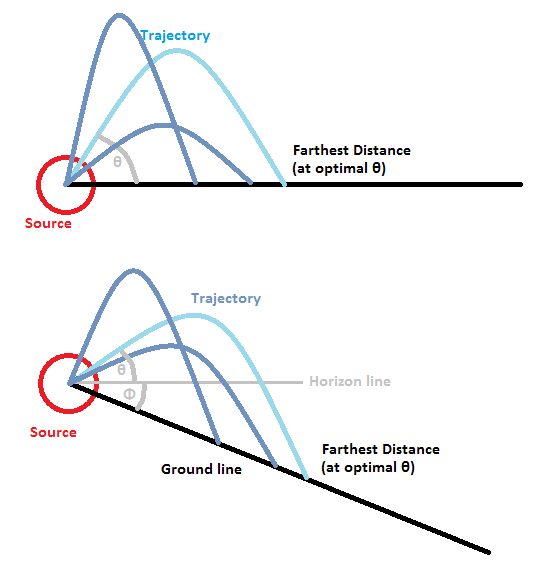
Visual representation of the problem - launching at a higher angle will reduce the object's x-velocity, while launching at a lower angle will reduce its time of flight. There is an optimum angle at which the object will travel the farthest from the origin.
Analysis
We start by considering the general path of an object in a uniform gravitational field, where we take a 2D slice along its path assuming no forces act perpendicular to its motion (this is already implicit in the above diagram). Within this 2D plane, any velocity that is perpendicular to the gravitational field will ideally have no force acting on it and is thus maintained. This axis will be called 'x' in this case. The axis that is parallel to the gravitational field will be acted upon by the field, and thus will experience acceleration. This is the 'y' axis. We can say at this point that Ax=0, Ay=-g (no acceleration in x, and gravity acceleration g downwards in y).
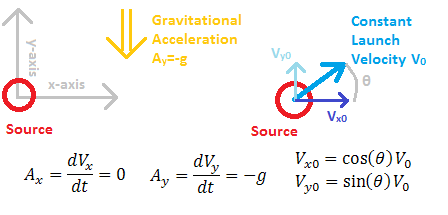
Setup of the problem, including axes, accelerations and velocities in two dimensions.
Then let the source be at the origin (0, 0). Finally, let the velocity with which the object is launched be a constant, V0. In the general case, the object could be launched at any angle from the origin, so define theta as the counter-clockwise angle from horizontal at which it is launched. Then Vx0=cos(theta)*V0, Vy0=sin(theta)*V0 are the x and y components of the launch velocity. Additionally, we let the ground surface (line in the 2D plane) be at an arbitrary angle phi (clockwise angle from horizontal), and the object is expected to land somewhere on this line. The distance away from the origin would then need to be calculated along this line, although it can be seen that for a finite line slope (not vertical) maximizing just the x component will be sufficient to determine the largest distance since y is proportional to x.
Next we find the path that the object follows over time (this is independent of the ground angle phi). Since time dependence is not important in this problem, we can cancel out the time variable by solving both x and y for time and then setting them equal to each other. Then what is obtained is a path function y=f(x, V0, theta). Start by integrating the two known accelerations Ax and Ay to get Vy=Vy0-gt, Vx=Vx0, with the initial velocity V0 and theta used as boundary conditions. Integrate again, and substitute the definitions of Vx0, Vy0 to obtain x(t, V0, theta)=V0*cos(theta)*t, y(t, V0, theta)=V0*sin(theta)*t-0.5*g*t^2. Then remove t dependence to get y(x, V0, theta)=tan(theta)*x-(g/(2*V0^2*cos(theta)^2))*x^2. This is the desired expression for the general path of an object.
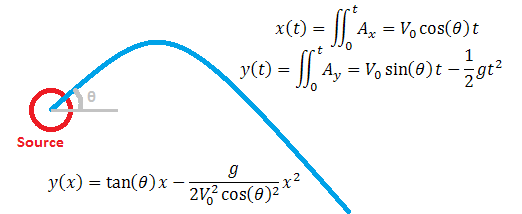
The equations for the path of the launched object are found. This represents the object in flight and is thus independent of the ground.
Next it is necessary to find where the object lands on the ground surface, which in this case is the intersection between the object path y(x) found above and the ground line defined by the angle phi. The function for the ground plane is y(x, phi)=-tan(phi)*x. Setting the two expressions equal to each other, we obtain the quadratic equation (g/(2*V0^2*cos(theta)^2))*x^2-(tan(phi)+tan(theta))*x=0. This gives two solutions, one at the origin (0, 0) as expected, since this is the starting point for the launch. The other intersection is at x=(2/g)*(tan(theta)+tan(phi))*V0^2*cos(theta)^2, and y can be determined from either of the above y(x) expressions. The simpler one is the ground line, and we can thus find the distance traveled along the ground by solving D=sqrt(x^2+y^2), or D(theta, phi, V0)=(2*V0^2/g)*(tan(phi)+tan(theta))*cos(theta)^2/cos(phi). However, this is still a bit complicated to use for optimization.
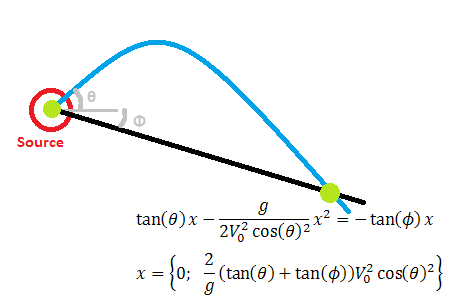
We find the two intersection points of the object with the ground - at the launch point (origin), and at the landing point. The latter will need to be used for optimization.
Solution
As mentioned previously, it will be sufficient to maximize x for the desired solution, and for the optimization it is possible to remove all variables that have a uniform effect to reduce complexity. Then the function to optimize for largest x is xo(theta, phi)=(tan(phi)+tan(theta))*cos(theta)^2. The optimization requires the derivative of that function in theta to be zero (assuming phi is constant). The derivative d(xo)/d(theta)=cos(2*theta)-2*tan(phi)*sin(theta)*cos(theta)=0 for maximum distance. Solving that, and applying some trigonometric identities, we find the wonderfully simple optimal launch angle theta(phi)=pi/4-phi/2. In other words, the launch angle should be the angle centered between the vertical gravitational force line and the ground plane (line). For a horizontal ground, the optimum launch angle is 45 degrees, for a ground sloping almost directly downwards, the optimum launch angle is near zero (towards horizontal), and for a ground sloping almost directly upwards, the optimum launch angle is near vertical. This makes intuitive sense and can be easily verified by experiment.
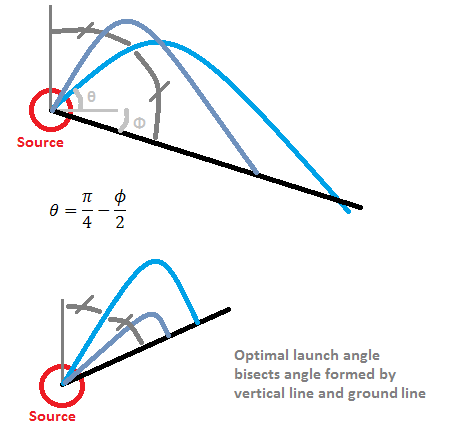
The optimal launch angle is represented graphically. It is simply the angle centered between the vertical line and the ground line.